Relationship to other projects/themes
The statistical methods developed in this Workpackage are central to the understanding of how uncertainty will be accommodated in nonlinear models. In particular there has been crossover work on Bayesian identification of backbone curves with WP 3.1. In addition there has been collaborative work on the energy harvesting devices being developed in Theme 5.
Aims
To develop Bayesian methods for nonlinear system identification and analysis in order to establish effective models validated over established levels of excitation.
Progress to date
The fundamental goal of WP 1.1 was to develop the methods which, using data from complex nonlinear systems, can be used to infer models which are robust against the uncertainties involved in the modelling process (milestone 4). These models can either be white-box (derived from the underlying physics of the problem), black-box (a data-based approximation whose parameters do not carry physical meaning) or grey-box – a hybrid using elements of white and black-box models. To realise this aim a Bayesian probabilistic framework was adopted. This is a powerful methodology which not only allows one to quantify the uncertainty in one’s parameter estimates, but can also evaluate the relative probability of competing model structures in a manner which prevents the selection of overly-complex models.
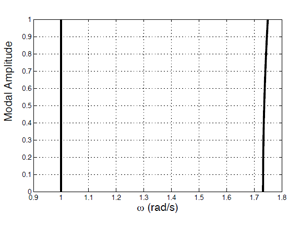
Figure 1: Backbone curves of a 2DOF system used for
Bayesian inference.
With this complete, the goal of WP 1.2 was then to develop the methods which allows one to propagate the identified uncertainties into future simulation, thus allowing one to make robust predictions. To achieve these aims extensive research was conducted into Markov chain Monte Carlo (MCMC) algorithms. These are powerful sampling algorithms which can be used to sample from complex probability distributions. They are particularly applicable to nonlinear identification problems as they facilitate the adoption of a Bayesian approach in situations where closed-form solutions are unavailable, and model simulations have to be relied upon. Furthermore, by providing a way of sampling from the probability distributions which arise during a Bayesian analysis, they allow one to propagate modelling uncertainties into future predictions simply through the use of Monte Carlo simulations. The major achievements which led to the completion of milestone 4 are summarised below.
Firstly, powerful MCMC algorithms from a variety of disciplines – many outside of engineering – have been interpreted and applied within the context of nonlinear structural dynamics [2,3,4,6]. Of particular note is Reversible Jump MCMC (RJMCMC) which has been incorporated by Daniela Tiboaca (whose PhD is aligned with the grant) and is currently being applied using data from the three-story test rig (shown in Figure 2 of WP 1.2). The power of RJMCMC lies in its ability to analyse the probability of the parameters within a set of models while also simultaneously analysing the probability of the models themselves.This ability allows it to compute the model evidence for a finite number of competing model structures at the same time as it updates their parameters. Secondly, a set of unique algorithms and methodologies have been developed which are designed to target issues which have been identified as the grant has progressed.
This has included the development of algorithms which have a relatively small computational cost [5,6] and can therefore be applied in situations where larger, more computationally demanding models are being employed. A particularly interesting issue which arose during collaborative projects was the issue of ‘Big Data’ – sets of measurements whose size make them difficult to manage. This issue was addressed using concepts from information theory which allowed the selection of small but ‘highly informative’ subsets of measurements from which it is possible to infer models with a high level of certainty [4,7,9].
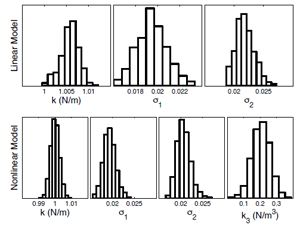
Figure 2: Posterior parameter samples of a linear
and nonlinear model inferred from backbone curve
data.
Current work is aiming to exploit this concept within the context of experimental design – identifying the excitations which will provide highly informative measurements [8]. Finally, the tools which have arisen from this research have been used to aid work with the other researchers and industrial partners of the grant. This has involved the development of probabilistic models of components of Advanced gas-cooled reactors [O1][O2], hysteretic systems (using grey-box models) and a rotation energy harvesting device developed as part of Theme 5. An interesting collaboration has also arisen between the current work and that being conducted in Theme 3 [1]. This has involved combining MCMC algorithms with the solutions derived using second-order normal forms to infer models from the backbone curves of nonlinear systems.
As an example, Figure 1 shows the backbone curves from a 2 degree-of-freedom system which possesses one linear mode and one nonlinear mode. In this case the nonlinearity is weak and only a slight amplitude dependence can be seen in the second mode. In such a case it is not clear whether one should use a linear or a relatively complex nonlinear model with more unknown parameters.
Figure 2 shows shows RJMCMC parameter estimates for linear and linear + cubic stiffness modal models for the second mode (the ‘sigma’ coefficients being precision parameters). In this case, the RJMCMC algorithm established a probability of 0.89 for the nonlinear (k,k3) model, compared to one of 0.11 for the linear (k only) model. An important point to note is that the correct model structure produced an unbiased estimate of the linear stiffness which is present in both models.