Relationship to other projects/themes
This workpackage is linked most strongly with the energy harvesting work being carried out in Theme 5. In addition there are strong connections to other workpackages, particularly WP1.1, WP1.2 and WP3.1 each involve models based on nonlinear modal analysis, and the variability and uncertainty modelling involved in WP2.1 will involve interaction with WP1.1 and WP1.2. In fact, as the treatment of nonlinear systems with random forcing is so different from deterministic nonlinear system, this workpackage has been inspiring researchers working in other themes to adopt these approaches. For example, we are now planning a Technical Workshop in 2015 to consider how randomly forced systems can be related to normal forms methods developed in WP 4.1 and then used in practice in WP 3.1.
Aims
To model random effects in nonlinear structural dynamics. And to understand the effects of nonsinusoidal forcing and other inputs to nonlinear systems.
Progress to date
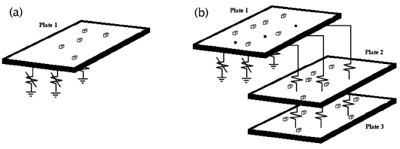
Figure 1: Investigated systems (a), single nonlinear plate; (b) 3 plate system coupled with linear springs, with nonlinear springs to ground. Any of the plates could have nonlinear springs to earth.
Dr Graham Spelman has been working on the development of a method to study the high frequency vibration of multi-modal nonlinear systems. The approach taken is based on an established technique for linear systems known as Statistical Energy Analysis (SEA). With this approach a complex system is divided into subsystems and the vibration level in each subsystem is described by a single energy variable. A set of algebraic equations governing the energy variables is derived by considering a power balance between power inputs, dissipation and energy transfer between subsystems. A typical linear SEA system is given in Figure 1 (in the absence of the nonlinear springs). Each plate is a subsystem with an associated energy variable.
The challenge is that the addition of nonlinear springs creates coupling between frequencies, allowing energy to flow between plates as well as between frequencies. The first step in developing nonlinear SEA, which we call NLSEA, was achieved for milestone MS5 at month 18 of the project. The NLSEA technique had been developed for a single nonlinear plate by dividing the total response energy into frequency bands (these frequency bands are now the subsystems): each frequency band has a single unknown energy level, and a set of nonlinear algebraic equations governing the energy levels are obtained.
The resulting equations represent an extension of SEA to the nonlinear regime. The nonlinear SEA approach summarised has been benchmarked against full time domain simulations of the plate structure of Fig 1(a) [3, 4]. When the structure is excited over a narrow frequency range, the nonlinearity cascades the response energy to a wider frequency range, and this phenomenon is well predicted by the method. Furthermore, the method predicts the mean of an ensemble of random systems, allowing the modelling of structures with uncertainty in the system parameters. This completed MS5 with the main deliverables as represented by the work in [3] and [4].
Since MS5, the nonlinear SEA approach has been extended to coupled systems: for instance the three plate system of Figure 1 (b). The total response is described by an extended set of energy variables: there is one energy degree-of-freedom for each frequency band, in each plate.
The linear power transfer between the plates in a given frequency band is described by conventional linear SEA parameters, while the power transfer between two frequency bands in a given plate is described by the new nonlinear analysis. The nonlinear SEA approach has shown very good agreement with full simulations at a small fraction of the computational cost [4]. An example result is given in Figure 2.
The case of a linear plate driven by an external force (random forcing up to 75 Hz), coupled to a nonlinear plate, coupled to a third linear plate, comparing results from the nonlinear SEA theory to a numerical benchmark.
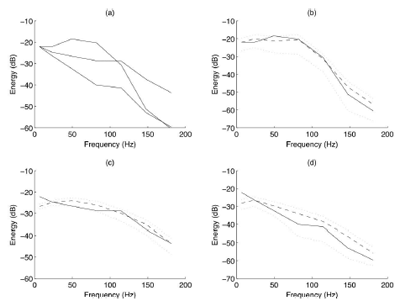
Figure 2: (a) Comparisons between subsystem energies, for the three-plate structure (second plate nonlinear), results are from the nonlinear SEA method. Forcing is onto the first plate, and the plates can be identified from decreasing energy through plates 1 to 3 in the frequency range up to 100 Hz. (b), (d), for plates 1, 3 respectively, comparison of the SEA prediction (solid) to the ensemble mean from the benchmark code (dashed), with a 2 sigma bound shown on the benchmark ensemble (light grey).
The driven plate (b) has an energy spectrum with frequency content primarily over the frequency range of excitation. This energy distribution is coupled into the nonlinear plate (c), at which point the nonlinearity operates and scatters energy into the higher frequency ranges, this distribution is then coupled into the third plate (d), and back to the first. It is of interest that the plate with the greatest energy at higher frequencies (above 75 Hz), is not the plate that is driven by external forces (note, plot (a)), it happens deeper in the structure. Additionally it highlights how difficult it is to isolate part of a structure from the effect of the nonlinearity, (and hence why it is so important to model it), despite the third plate being linear, it is strongly affected by nonlinearity elsewhere in the structure. Extensions to the work will include:
- prediction of the ensemble variance in addition to the ensemble mean
- the modelling of structures with nonlinear joints
- the development of methods to embed the NLSEA technique into larger linear models as has already been achieved for the traditional linear SEA methods.
Work by Professor Robin Langley on nonlinear random vibration under wide band loading has led to a new bound on the performance of energy harvesting devices [1,2]. This is linked to work in Theme 5, and collaborative work with colleagues in Southampton has been performed on nonlinear damping. Work on nonlinear random vibration is being continued by the associated PhD students David Hawes and Demetris Demetriou. This includes work on functional series which will link to experimental methods in Theme 3.