Relationship to other projects/themes
The techniques in WP 3.1 are being developed in tandem with the WP 3.2 experimental work. Other links include WP 4.1, the development of a systematic way to compute backbone curves has been built on the normal form method developed in 4.1, and WP 1.1 through P. Green which has led to work on using Bayesian identification methods via backbone curves [6].
Aims
To develop the theoretical framework and testing methods required to enable nonlinear modal analysis and testing to be viable for full-scale industrial structures.
Progress to date
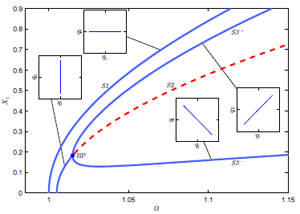
Figure 1: Response of a nonlinear 2 DoF system. X1 is amplitude of DOF 1, Ω is response frequency
It is well-known that nonlinear structures exhibit amplitude-dependent response frequencies and, if projected onto the linear modes, coupling between those modes. These observations have led to the development of techniques for the analysis of backbone curves, which captures resonances and modal interactions of the underlying undamped structure. Work in this area has, almost universally, been numerical; whereas the approach adopted here is to analytically study weakly nonlinear structures. This has allowed us to identify and understand various mechanisms for nonlinear behaviour, and based on this, develop a framework through which numerical models can be calibrated and corrected (hence to feed into WP 3.3) using experimental data (acquired using methods developed in WP 3.2).
Specifically, we have used the second-order normal form method, proposed by Neild and Wagg (Proc. Royal Society Part A , 467, 2011) and extended in WP 4.1, to identify and understand interactions between the linear modes due to nonlinearities. The method allows the study of both the fundamental response of the system, and the contributions from harmonics.
Taking a nonlinear model of a structure, an approach has been developed to decompose the response into a set of equations relating to the underlying resonant backbone curves using a matrix formulation [1,2,3]. In contrast to those for linear systems, backbone curves for nonlinear systems can contain more than one linear mode and there may be more backbone curves than degrees-of- freedom. In addition, these backbone curves can arise from contributions of the linear modes which are out-of-unison [4,5].
We have shown that both bifurcations of the backbone curves [1] and isolated backbone curves can exist [6] and demonstrated the mechanisms for this. Figure 1 shows example backbone curves for a system including bifurcation and the nonlinear mode shapes for various responses (inset panels) [5].
To date, we have applied our analytical approach to systems with 2 or 3 interacting linear modes, for which the algebra is manageable by hand. To allow us to handle more interacting modes a computer programme is now being developed to algebraically derive the equations.
Additional insight has been gained by considering the types of terms present in the backbone curve equations. We have shown that terms that enforce a specific phase relationship (phase-locking) between linear modes are needed for internal resonance to occur.
Now we are working towards demonstrating that phase-locking is required for nonlinear normal modes (the response on a backbone curve) to be indicative of the forced responses, in contrast to recent literature which treats them as any periodic response. Also of interest is the influence of the nonlinear terms in non-phase-locked systems, which can have the effect of changing the apparent linear stiffness. Our methods are able to describe and compensate for this phenomenon.
Since the forced, damped responses are of most practical interest, it is important to link these to the backbone curves. An energy-based technique has been developed that uses the backbone curves to predict the resonant peaks of the forced responses [7]. These resonant peaks do not necessarily occur when forcing is 90◦ out-of-phase with the response, as is the case with linear systems, due to energy transfer between the linear modes [8]. These advances form a framework for modal analysis, and therefore achieved milestone MS6, with papers [5], [7] & [8] representing the key Deliverables. Building on these insights, work has been conducted on identifying nonlinear parameters using measured response data.
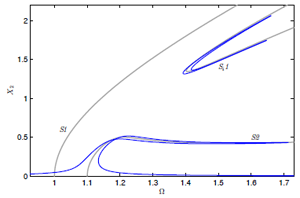
Figure 2: Forced response of fitted model. X2 is amplitude of DOF 2, Ω is forcing frequency
The approach uses an uncalibrated numerical model of the structure and measured resonant decay responses to approximate the backbone curves (see WP 3.2). Employing the techniques outlined above, analytical expressions for the backbone curves are found and the measured data is used to provide the response frequency and amplitude. This data may be fitted to the backbone curve expressions to calibrate the relevant nonlinear terms.
This approach may be conducted using a least-squares fitting, however we have found that the MCMC algorithm (see WP 1) [9] is far more robust and provides valuable insight into which nonlinear terms may be removed from the model due to their relative insignificance. A machine learning approach was also developed — see Dervilis et al. (2014) in WP 1.2. Figure 2 shows numerical simulations of the forced responses of a 2-mode system, using an identified model, alongside the underlying backbone curves of the exact model [6]. The forced responses of the identified model follow the backbone curves closely (and also match the forced responses of the exact model).
Note our approach has also identified the presence of an isola. This approach is now being applied to experimental data, see WP 3.2 progress report. It is also being compared to broad-band excitation data fitting techniques, being developed in WP 1. Other current work in this area includes extending the approach to systems with non-polynomial nonlinearities, with a greater number of interacting modes and with nonlinear damping terms.